일반 배열에서 '선형 검색'을 할 때는 모든 원소들을 쭉 찾아야 하기 때문에 O(N) 단계가 걸린다.
만약 정렬이 되어있다면 '이진 검색'을 수행할 수 있어 O(logN)이 걸려 훨씬 빨라진다.
그러나 이보다 훨씬 더 좋아질 수 있다. '해시 테이블'을 이용하면 O(1) 만에 검색이 가능하다. 해시 테이블의 동작 방법, 사용처를 알면 많은 상황에서 해시 테이블의 엄청난 검색 속도를 활용할 수 있다.
8. 1 해시 테이블
대부분의 프로그래밍 언어는 '해시 테이블(hash table)'이라는 자료 구조를 포함하며, 빠른 검색 속도가 장점이다.
해시 테이블은 쌍으로 이뤄진 값들의 리스트다. 첫 번째 항목을 '키(key)'라 부르고, 두 번째 항목을 '값(value)'이라 부른다. 해시 테이블에서 키와 값은 서로 중요한 관계다.
해시 테이블의 값 룩업은 딱 한 단계만 걸리므로 평균적으로 효율성이 O(1)이다.
8. 2 해시 함수로 해싱
A = 1B = 2C = 3D = 4E = 5...
ACE = 135
CAB = 312
위 예시와 같이, 특정 문자를 가져와 숫자로 변환하는 과정을 '해싱(hasing)'이라 부른다.
또한 글자를 특정 숫자로 변환하는 데 사용한 코드를 '해시 함수(hash function)'라 부른다.
예를 들어 해시 함수가 '곱하기(*)'인 경우, ACE는 1 * 3 * 5 = 15가 된다.
해시 함수는 동일한 문자열을 해시 함수에 적용할 때마다 항상 동일한 숫자로 변환해야 한다. 즉, 반환하는 결과가 일관되어야 한다. 그래서 난수나 현재 시간을 계산에 넣는 해시 함수는 유효하지 않다. 매 번 다른 값이 나오기 때문이다.
8. 3 재미와 이익, 특히 이익을 남길 유의어 사전 만들기
유의어 사전을 만드는 과정이 해시 테이블의 좋은 사용 사례이다.
해시 테이블은 배열과 유사하게 내부적으로 데이터를 한 줄로 이뤄진 셀 묶음에 저장한다.
그리고 각 셀마다 주소가 있다.
[ 1 ] |
[ 2 ] |
[ 3 ] |
[ 4 ] |
[ 5 ] |
[ 6 ] |
[ 7 ] |
[ 8 ] |
[ 9 ] |
[ 10 ] |
만약 "곱셈" 해시 함수를 이용한다고 가정해보자.
첫 번째 항목을 해시 테이블에 추가한다.
{"bad" => "evil"}
컴퓨터는 키에 해시 함수를 적용한다.
bad = 2 * 1 * 4 = 8
키("bad")는 8로 해싱되므로 컴퓨터는 값("evil")을 셀 8에 넣는다.
[ 1 ] |
[ 2 ] |
[ 3 ] |
[ 4 ] |
[ 5 ] |
[ 6 ] |
[ 7 ] |
"evil" [ 8 ] |
[ 9 ] |
[ 10 ] |
두 번째 항목을 해시 테이블에 추가한다.
{"cab" => "taxi"}
컴퓨터는 키에 해시 함수를 적용한다.
cab = 3 * 1 * 2 = 6
키("cab")는 6으로 해싱되므로 컴퓨터는 값("taxi")을 셀 6에 넣는다.
[ 1 ] |
[ 2 ] |
[ 3 ] |
[ 4 ] |
[ 5 ] |
"taxi" [ 6 ] |
[ 7 ] |
"evil" [ 8 ] |
[ 9 ] |
[ 10 ] |
8. 4 해시 테이블 룩업
해시 테이블에서 항목을 검색할 때는 키를 사용해서 연관된 값을 찾는다.
만약 키 "bad"의 값을 검색하고 싶다고 하자. 그러면 컴퓨터는 "bad"의 값을 찾기 위해 두 단계를 실행한다.
(1) 컴퓨터는 룩업 하고 있는 키를 해싱한다. BAD = 2 * 1 * 4 = 8
(2) 결과가 8이므로 셀 8을 찾아가서 지정된 값을 반환한다.
해시 테이블에서 각 값의 위치는 키로 결정된다. 즉, 키 자체를 해싱해 키와 연관된 값이 놓여야 하는 인덱스를 계산하므로 키 자체로 값을 어디서 찾을 수 있는지 안다.
컴퓨터는 키를 해싱해서 숫자로 바꾼 후 그 수의 인덱스로 바로 가서 저장된 값을 추출한다. 이것이 해시 테이블의 값 룩업이 O(1)인지의 이유다.
해시 테이블에선 '단방향(one-directional) 룩업'만 가능하며, 한 단계만에 값을 찾기 위해선 그 값의 키를 알아야 한다. 키를 모르면 해시 테이블 내 모든 키/값 쌍을 검색해야 하고, 결국 O(N)이다. 거꾸로 값을 이용해 연관된 키를 찾을 때도 빠른 검색 기능을 사용할 수 없다.
8. 5 충돌 해결
해시 테이블에는 문제도 있다.
만약 해시 함수를 사용해서 나온 인덱스에 이미 기존 값이 저장되어 있으면 어떻게 할까?
예를 들어, "dab"란 키를 해싱하면 DAB = 4 * 1 * 2 = 8 이 나온다. 그리고 "pat"를 해시 테이블 셀 8에 추가하려고 하니 이미 셀 8에 "evil"이 들어 있다.
[ 1 ] |
[ 2 ] |
[ 3 ] |
[ 4 ] |
[ 5 ] |
"taxi" [ 6 ] |
[ 7 ] |
"evil" [ 8 ] |
[ 9 ] |
[ 10 ] |
이미 채워진 셀에 데이터를 추가하는 것을 "충돌(collision)"이라 한다.
이를 해결하는 고전적 방법이 있다. "분리 연결법(seperate chaining)"이다. 충돌이 발생했을 때 셀에 하나의 값을 넣는 대신 '배열'로 참조를 넣는 방법이다.
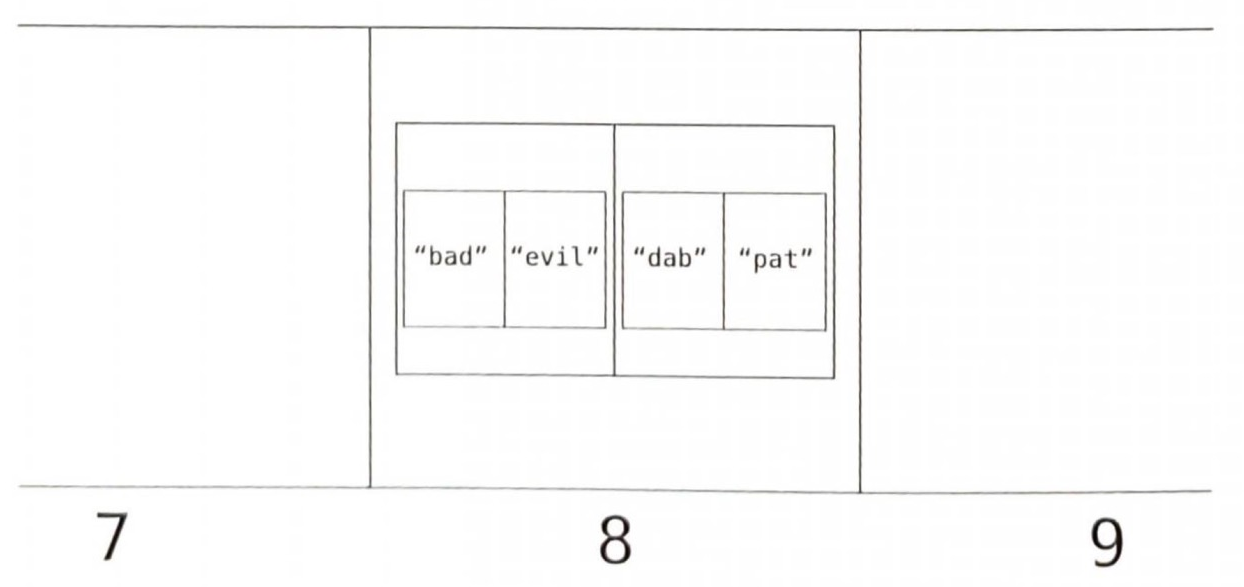
이 배열의 인덱스 8에 포함된 하위 배열의 첫 번째 값은 단어, 두 번째 단어는 그 단어의 동의어다.
이렇게 바꾸면 해시 테이블은 다음 단계를 거쳐 룩업 한다.
(1) 컴퓨터는 키를 해싱한다. DAB = 4 * 1 * 2 = 8
(2) 셀 8을 룩업 하니 셀 8이 하나의 값이 아닌 배열들의 배열을 포함하고 있음을 안다.
(3) 각 하위 배열의 인덱스 0을 찾아보며 ("dab")을 찾을 때까지 배열을 차례대로 검색한다.
(4) 일치하는 하위 배열의 인덱스 1에 있는 값을 반환한다.
만약 모든 데이터가 해시 테이블의 한 셀에 들어가게 된다면 해시 테이블은 배열보다 나을 게 없는 사실상 O(N)이다. 그렇기 때문에 해시 테이블에 충돌이 거의 없도록 디자인해야 한다.
8. 6 효율적인 해시 테이블 만들기
해시 테이블은 다음 세 요인에 따라 효율성이 정해진다.
- 해시 테이블에 얼마나 많은 데이터를 저장하는가?
- 해시 테이블에서 얼마나 많은 셀을 쓸 수 있는가?
☞ 당연히 적은 셀에 많은 데이터를 저장하면 충돌이 많을 테고 효율성이 떨어진다.
- 어떤 해시 함수를 사용하는가?
☞ 좋은 해시 함수란 사용 가능한 모든 셀에 데이터를 분산시키는 함수다. 데이터를 넓게 퍼뜨릴수록 충돌이 적다.
충돌 횟수가 줄어들수록 해시 테이블의 효율성이 높아진다. 또한 많은 메모리를 낭비하지 않으면서 균형을 유지해야 한다.
'부하율(load factor)'은 데이터와 셀 간의 비율이다. 이상적인 부하율은 0.7(원소 7개 / 셀 10개)이다. 만약 해시 테이블에 저장된 데이터가 7개면 셀은 10개여야 하고, 원소가 14개면 셀은 20개 있어야 한다.
이를 통해 효율성 O(1)의 뛰어난 룩업이 가능하다.
8. 7 해시 테이블로 데이터 조직
해시 테이블은 데이터를 쌍으로 저장하므로 데이터를 조직하는 많은 케이스에 유용하다.
예를 들어 각 품목의 재고를 기록하는 재고 관리 시스템을 다음과 나타낼 수 있다.
{"Yellow Shirt" => 1203, "Blue Jeans" => 598, "Green Felt Hat" => 65}
해시 테이블은 다양한 속성을 갖는 객체를 표현할 때도 흔히 쓰인다. 각 속성은 속성명이 키고 실제 속성이 값인 쌍으로 된 데이터다. 예를 들어 개를 다음처럼 표현할 수 있다. 배열 안에 여러 해시 테이블을 넣어 개 목록을 생성한다.
[
{"Name" => "Fido", "Breed" => "Pug", "Age" => 3, "Gender" => "Male"},
{"Name" => "Lady", "Breed" => "Poodle", "Age" => 6,"Gender" => "Female"},
{"Name" => "Spot", "Breed" => "Dalmatian", "Age" => 2,"Gender" => "Male"}
]8. 8 해시 테이블로 속도 올리기
해시 테이블은 쌍으로 된 데이터와 완벽하게 맞지만, 쌍이 아닌 데이터라도 코드를 빠르게 만들 때 쓰인다.
만약에 어떤 배열이 있다.
int[] arr = {61, 30, 91, 11, 54, 38, 72};
위 배열에서 어떤 수를 찾으려면 O(N)이 필요하다.
하지만 위 수 배열을 다음과 같은 해시 테이블로 변환해보자. 각 수를 키로 저장해서 각 수와 연관된 값에 boolean true를 할당한다.
[61 => true, 30 => true, 91 => true, 11 => true, 54 => true, 38 => true, 72 => true]
어떤 수를 키로 하여 위 해시 테이블을 검색하면 한 단계 만에 숫자를 룩업 할 수 있다. 예를 들어 72를 키로 사용하면 72의 값이 true이니 true를 받는다. 이처럼 해시 테이블 룩업은 한 단계만 필요하므로 해시 테이블에서는 어떤 수든 한 단계만에 찾을 수 있다.
배열을 해시 테이블로 바꾸면 O(N) 검색이 O(1) 검색으로 바뀐다.
해시 테이블을 "인덱스"로 사용하는 기법은 배열을 여러 번 검색해야 하는 알고리즘에 자주 쓰인다. 키가 해시 테이블로 룩업 해서 어떤 값이든 받으면 그 키가 해시 테이블에 있다는 뜻이기 때문이다.
8. 9 마무리
해시 테이블의 O(1) 읽기와 삽입은 굉장히 좋은 장점이며, 효율적인 자료 구조다.
다음 파트에선 코드의 간결성과 유지보수성을 향상할 수 있는 두 자료 구조를 알아본다.

해당 글은 '누구나 자료구조와 알고리즘' 책의 내용을 기반으로 작성되었습니다.
오로지 학습용으로 작성하였음을 밝힙니다.
더 자세한 내용을 확인하고 싶다면 해당 저서를 참고하시길 바랍니다.
'자료구조 & 알고리즘' 카테고리의 다른 글
| Ch.10 재귀를 사용한 재귀적 반복 (도서 요약 "누구나 자료구조와 알고리즘") (0) | 2022.06.06 |
|---|---|
| Ch.09 스택과 큐로 간결한 코드 생성 (도서 요약 "누구나 자료구조와 알고리즘") (0) | 2022.05.11 |
| Ch.07 일상적인 코드 속 빅 오 (도서 요약 "누구나 자료구조와 알고리즘") (0) | 2022.05.05 |
| Ch.06 긍정적인 시나리오 최적화 (도서 요약 "누구나 자료구조와 알고리즘") (0) | 2022.05.05 |
| Ch.05 빅 오를 사용하거나 사용하지 않는 코드 최적화 (도서 요약 "누구나 자료구조와 알고리즘") (0) | 2022.05.03 |



